Lex Theory

During the first phase the compiler reads the input and converts strings in the source to tokens. With regular expressions we can specify patterns to lex so it can generate code that will allow it to scan and match strings in the input. Each pattern in the input to lex has an associated action. Typically an action returns a token that represents the matched string for subsequent use by the parser. Initially we will simply print the matched string rather than return a token value.

The following represents a simple pattern, composed of a regular expression, that scans for identifiers. Lex will read this pattern and produce C code for a lexical analyzer that scans for identifiers.

letter(letter|digit)*

This pattern matches a string of characters that begins with a single letter followed by zero or more letters or digits. This example nicely illustrates operations allowed in regular expressions:

repetition, expressed by the "*" operator
alternation, expressed by the "|" operator
concatenation

Any regular expression expressions may be expressed as a finite state automaton (FSA). We can represent an FSA using states, and transitions between states. There is one start state and one or more final or accepting states.

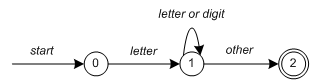
Figure 3: Finite State Automaton

In Figure 3 state 0 is the start state and state 2 is the accepting state. As characters are read we make a transition from one state to another. When the first letter is read we transition to state 1. We remain in state 1 as more letters or digits are read. When we read a character other than a letter or digit we transition to accepting state 2. Any FSA may be expressed as a computer program. For example, our 3-state machine is easily programmed:

start:  goto state0

state0: read c
        if c = letter goto state1
        goto state0

state1: read c
        if c = letter goto state1
        if c = digit goto state1
        goto state2

state2: accept string

This is the technique used by lex. Regular expressions are translated by lex to a computer program that mimics an FSA. Using the next input character and current state the next state is easily determined by indexing into a computer-generated state table.

Now we can easily understand some of lex’s limitations. For example, lex cannot be used to recognize nested structures such as parentheses. Nested structures are handled by incorporating a stack. Whenever we encounter a "(" we push it on the stack. When a ")" is encountered we match it with the top of the stack and pop the stack. However lex only has states and transitions between states. Since it has no stack it is not well suited for parsing nested structures. Yacc augments an FSA with a stack and can process constructs such as parentheses with ease. The important thing is to use the right tool for the job. Lex is good at pattern matching. Yacc is appropriate for more challenging tasks.