Open Hashing
A hash table is simply an array that is addressed via a hash function.
For example, in Figure 1, HashTable is an array with 8 elements. Each element
is a pointer to a linked list of numeric data. The hash function for this example simply divides
the data key by 8, and uses the remainder as an index into the table. This yields a number
from 0 to 7. Since the range of indices for HashTable is 0 to 7, we are guaranteed
that the index is valid.
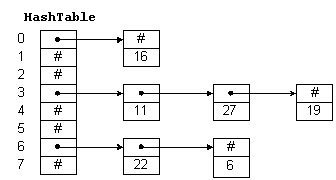
Figure 1: A Hash Table
To insert a new item in the table, we hash the key to determine which list the item goes
on, and then insert the item at the beginning of the list. For example, to insert 11, we divide
11 by 8 giving a remainder of 3. Thus, 11 goes on the list starting at HashTable(3).
To find a number, we hash the number and chain down the correct list to see if it is in the
table. To delete a number, we find the number and remove the node from the linked list.
Entries in the hash table are dynamically allocated and entered on a linked list associated with each hash table entry. This technique is known as chaining. If the hash function is uniform, or equally distributes the data keys among the hash table indices, then hashing effectively subdivides the list to be searched. Worst-case behavior occurs when all keys hash to the same index. Then we simply have a single linked list that must be sequentially searched. Consequently, it is important to choose a good hash function. The following sections describe several hashing algorithms.
Table Size
Assuming n data items, the hash table size should be large enough to accommodate a reasonable number of entries. Table 1 shows the maximum time required to search for all entries in a table containing 10,000 items.
| size | time (ms) |
|---|---|
| 1 | 23544 |
| 10 | 2473 |
| 100 | 331 |
| 1,000 | 100 |
| 10,000 | 70 |
A small table size substantially increases the time required to find a key. A hash table may be viewed as a collection of linked lists. As the table becomes larger, the number of lists increases, and the average number of nodes on each list decreases. If the table size is 1, then the table is really a single linked list of length n. Assuming a perfect hash function, a table size of 2 has two lists of length n/2. If the table size is 100, then we have 100 lists of length n/100. This greatly reduces the length of the list to be searched. There is considerable leeway in the choice of table size.